先来个宏观上的理解：

其实这块逻辑是个标准流程，而且其他地方介绍的也很多了，这里简单提下。

坐标转换，其实是不同坐标系之间的变换，一个渲染顶点，要想让它呈现在屏幕上的某个位置，是需要让这个顶点经过一个个坐标系的变换来进行的，每经过一个坐标系，它的坐标就会使用矩阵来执行变化一次，最终变化成为屏幕上的位置。

第一个Object Coordinates，这个比较好理解，就是模型的局部坐标系。这种坐标一般是美术建模的时候就会设定的，当然使用程序代码绘制出来的坐标自然是代码指定的。

比方说，一个坦克，美术在设计时，模型的几何中心点就作为了整个模型的坐标原点，那么炮管上某个顶点的位置就是相对于几何中心的一个偏移，假定为（0,1,1）。

第二个World Coordinates。还是坦克的例子，当游戏运行时，显然是会把坦克摆放在场景里的某个出生点位置，假定为（500,500,1000）的位置，这个位置是相对于整个关卡的原点的。这一步的坐标变换，就是要计算出指定顶点相对于这个关卡原点的坐标。这个就是世界坐标了。

第三个Eye Coordinates。到这一步，坐标原点变成了摄像机的位置，以摄像机为原点，计算出指定顶点的坐标。

第四个Clip Coordinates。这一步最重要的是投影矩阵的构建，这个矩阵的推导过程，，是应该要仔细研究下。重要的是带了个w参数，用来计算下一步的NDC

所谓投影，就是投到了近裁剪面上。

 

 

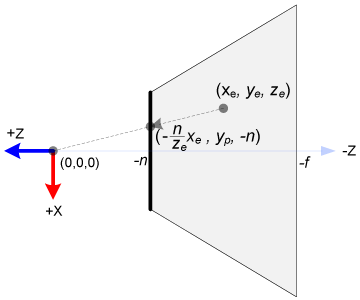
 第五个，Normal Device Coordinates.

 

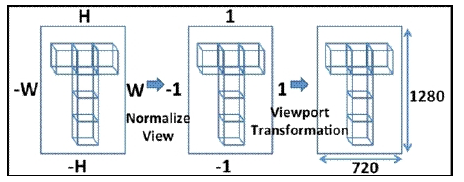
这个图仅供参考。其实就是把上一步计算出来的坐标，映射成一个比例关系的坐标，这个比例是这样对应的，假设视锥体的四个面为Left,Right,Bottom,Top,Near,Far

X域的值，从 [Left,Right] 映射到 [-1,1]

Y域的值，从 [Bottom,Top] 映射到 [-1,1]

Z域的值，从 [Near,Far] 映射到 [-1,1]

如果指定的顶点在视锥体里，就会被映射到这个Cube里，这个坐标系的中心点是（0 ，0， 0）。

第六个，windon coordinates.其实就是窗口坐标转换了。